どうも!初めましての方は初めまして、初心者のWebサイト勉強のとみーです!
再生過程は、確率的に発生するイベントについて、イベントの発生数がどうなっていくかを観測するモデルです。
電車やバスの到着数や、窓口にやってきた客の人数などをモデル化することができます。

新たなイベントが発生するたびに $M(t)$ が+1されるという、非常にシンプルなモデルです。
しかし、裏を返せばイベントが発生したときに+1以外の変化が起こるようなものをモデル化することができません。
例えば所持金は買い物をするたびに買った金額だけ減り、お小遣いやお給料が手に入るとその分だけ増えますよね。この場合、所持金の増え幅・減り幅は+500だったり、–1000だったりするので、再生過程では扱うことができません。
参考 再生過程の基本については、こちらの記事で分かりやすくまとめてあります。
そこで、+1以外の変化も追えるようにしたのが再生報酬過程です。
イベントが発生したときの報酬・コストを考えることで、通常の再生過程では扱えなかったより多様な変化をモデル化できるようになるのが特徴です。
参考 再生報酬過程の基本については、こちらの記事で分かりやすくまとめてあります。
しかし、実はこの再生報酬過程でもまだ扱えないものが多くあります。

そして、それを補うためのアイデアが部分報酬・部分コストです。
今回は、その部分報酬・部分コストについて分かりやすく解説していきます!
確率の基本的な知識がある方(高校数学〜大学入門)
再生報酬過程-部分報酬モデルとは
イメージをしやすくするために、具体例を使って考えましょう。
条件・設定
スーパーマーケットのレジには客が1人ずつ並び列を作ります。

会計が済んだら客は列を離れ、次の客の会計を行います。
このとき、レジに列を作っている待ち人数をモデル化したいとし、変数を次のように置きます。
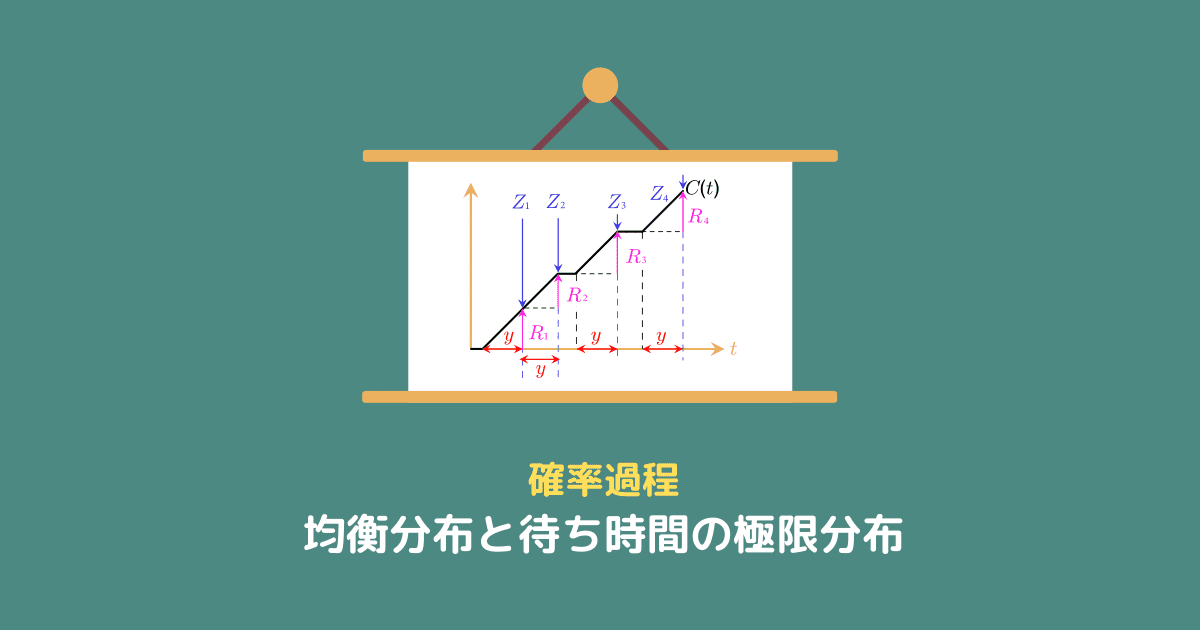
次の図のようなイメージです。
このとき、
待ち人数は会計開始時刻 $\{Z_n\}$ に関係なく変動する
ことに注意しましょう。
レジに並ぶタイミングはバラバラですし、別のレジの方が空いていると思った客が列から抜けていくこともあります。
再生報酬過程は時刻 $\{Z_n\}$ で変化する値に注目するので、このように自由に変わってしまう値を追うのには適していません。

しかし、少し工夫して再生報酬過程に落とし込むことはできます!
そのためには、報酬の定義を少し変える必要があります。
部分報酬モデルの報酬 $\{R_n\}$
再生報酬過程では、時刻 $Z_n$ にもらえる報酬を $R_n$ と定義していました。
しかし、今回のように時刻 $Z_n$ とは関係なく報酬の値が変わっていく場合、時刻 $Z_n$ に報酬がもらえるとは限りません。
そこで、報酬 $\{R_n\}$ を次のように定義します。
$$R_n=\mbox{時刻} Z_{n} \mbox{の累積報酬}-\mbox{時刻} Z_{n-1} \mbox{の累積報酬}$$
報酬の直感的なイメージ
新しい定義の報酬は、下の図を見ると分かりやすいです(赤矢印が報酬)。
$R_1 = 1$、$R_2 = 0$、$R_3 = 1$ です。
図的に捉えると、前の矢印の先頭から高くなった分が報酬です。
部分報酬モデル
上の図から分かる通り、途中で色々増えたり減ったりはするけど、
考えるのは時刻 $\{Z_n\}$ の部分だけ
にしましょう、というのが部分報酬モデルです。

言葉は難しく感じますが、仕組みがわかってしまえば単純ですね。
全部の変化を追うのではなく、$\{Z_n\}$ の部分だけを追うので部分報酬というのですね。
部分報酬モデルと再生報酬定理
部分報酬モデルは再生報酬過程の特殊なケースなので、再生報酬定理が成り立ちます。
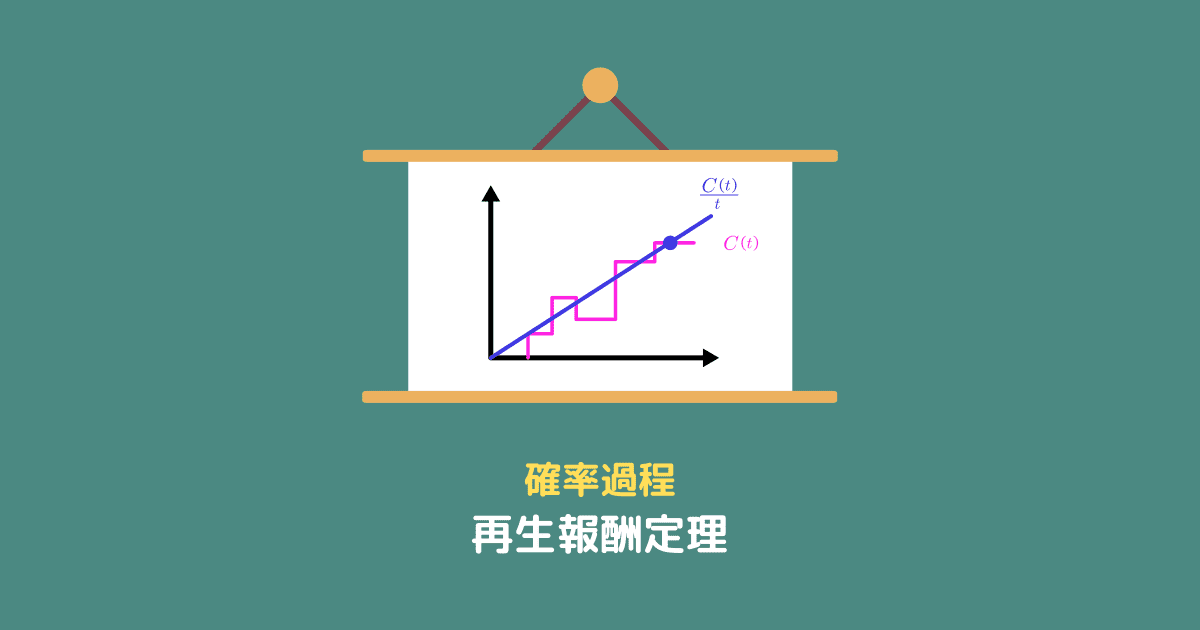
再生報酬定理
すべての自然数 $n$ に対し、$\mathbb{E}[X_n] = \frac{1}{\mu} < \infty, \mathbb{V}[X_n] < \infty$、$\mathbb{E}[R_n] < \infty$ が成り立つとき、
- $\displaystyle \frac{C(t)}{t} \xrightarrow[t \to \infty]{a.s.} \mu \mathbb{E}[R_n]$
- $\displaystyle \lim_{t \to \infty} \frac{c(t)}{t} = \mu \mathbb{E}[R_n]$
となる。
$C(t)$ は再生報酬過程($\sum_{i=1}^{M(t)}$)、$c(t)$ は再生報酬関数です。
参考 再生報酬定理については、こちらの記事で解説しています。

厳密には再生報酬過程とは少し異なるので、興味がある方のために最後に証明を載せておきます。
証明
報酬 $R_n$は時刻 $Z_n$ における累積報酬と時刻 $Z_{n-1}$ における累積報酬の差だが、これは言い換えると
期間 $X_n$ 中の総報酬と総コストの和
である。
区間内の総報酬を $P_n$、総コストを $N_n$ とすると、
$$R_n = P_n + P_n$$
となる。
ここで、
$$C(t) = \sum_{i=1}^{M(t)} R_i + \mbox{区間}[Z_{M(t)}, t] \mbox{の報酬}$$
なので、
$$\color{#FF21E3}{\sum_{i=1}^{M(t)}R_i + N_{M(t)+1}} \color{black}\leq C(t) \leq \color{#28AD00}{\sum_{i=1}^{M(t)}R_i + P_{M(t) + 1}}$$
が成り立つ。
各辺を $t$ で割ると、
$$\frac{\sum_{i=1}^{M(t)}R_i + N_{M(t)+1}}{t} \leq \frac{C(t)}{t} \leq \frac{\sum_{i=1}^{M(t)}R_i + P_{M(t) + 1}}{t}$$
このとき、再生報酬定理より
$$\frac{\sum_{i=1}^{M(t)}R_i + N_{M(t)+1}}{t} \xrightarrow[t \to \infty]{a.s.} \mu \mathbb{E}[R_n]$$
$$\frac{\sum_{i=1}^{M(t)}R_i + P_{M(t)+1}}{t} \xrightarrow[t \to \infty]{a.s.} \mu \mathbb{E}[R_n]$$
よって、はさみうちの原理から
$$\frac{C(t)}{t} \xrightarrow[t \to \infty]{a.s.} \mu \mathbb{E}[R_n]$$
同様に
\begin{eqnarray} \frac{\mathbb{E}[\sum_{i=1}^{M(t)}R_i + N_{M(t)+1}]}{t} \leq &\frac{c(t)}{t}& \leq \frac{\mathbb{E}[\sum_{i=1}^{M(t)}R_i + P_{M(t) + 1}]}{t} \\ \frac{M(t)\mathbb{E}[R_i] + \mathbb{E}[N_{M(t)+1}]}{t} \leq &\frac{c(t)}{t}& \leq \frac{M(t)\mathbb{E}[R_i] + \mathbb{E}[P_{M(t) + 1}]}{t} \\ \frac{M(t)}{t}\mathbb{E}[R_i] + \frac{\mathbb{E}[N_{M(t)+1}]}{t} \leq &\frac{c(t)}{t}& \leq \frac{M(t)}{t}\mathbb{E}[R_i] + \frac{\mathbb{E}[P_{M(t) + 1}]}{t} \\ \end{eqnarray}
で、極限をとると
\begin{eqnarray} \color{red}\lim_{t \to \infty} \frac{c(t)}{t} \color{black}&=& \lim_{t \to \infty} \left(\frac{M(t)}{t}\mathbb{E}[R_i] + \frac{\mathbb{E}[N_{M(t)+1}]}{t} \right) \\ &=& \lim_{t \to \infty} \left(\frac{M(t)}{t}\mathbb{E}[R_i] + \frac{\mathbb{E}[P_{M(t) + 1}]}{t} \right) \\ &=& \color{red}\mu \mathbb{E} [R_n] \end{eqnarray}

コメント
The next time I read a blog, Hopefully it doesnt fail me just as much as this particular one. After all, Yes, it was my choice to read, but I really believed youd have something useful to talk about. All I hear is a bunch of crying about something you can fix if you werent too busy looking for attention.