どうも!初めましての方は初めまして、初心者のWebサイト勉強のとみーです!
再生過程には、再生過程と再生関数の極限に関する性質を示す基本再生定理(Elementary Renewal Theorem:ERT)という定理が存在します。

今回は、その基本再生定理について解説します!
確率の基本的な知識がある方(高校数学〜大学入門)
イメージをしやすくするために、電車の到着を題材として
という風に変数を置きます。
参考 再生過程の基本や電車の題材の詳しい説明は、こちらの記事をご覧ください。
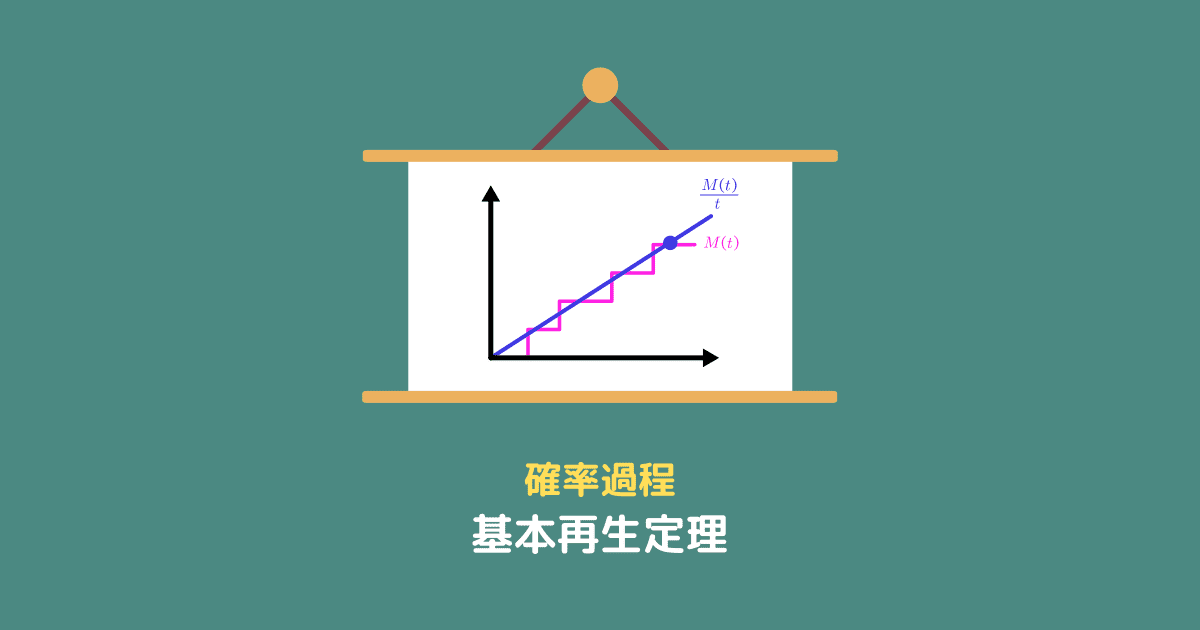
図にすると、次のような感じです。
基本再生定理(ERT)とは
基本再生定理の導出・理解のために必要な
確率変数の概収束
についてはじめに押さえましょう。
確率変数の概収束(ほとんど確実に収束)
基本再生定理は概収束を使った定理なので、概収束のイメージを掴んでおきましょう。
確率変数列 $\{X_n\}_{n \in \mathbb{N}}$ と確率変数 $X$ が
$$\mathbb{P} \left( \lim_{n \to \infty} X_n = X \right) = 1$$
を満たすとき、$\{X_n\}$ は $X$ に概収束(ほとんど確実に収束)するといい、
$$X_n \xrightarrow[n \to \infty]{a.s.} X$$
と表す。

概収束は、収束する確率が1という意味です。
基本再生定理
基本再生定理とは、再生過程・再生関数の極限に関する次の関係のことです。
2以上のすべての整数 $n$ に対し、$\mathbb{E} [X_n]= \frac{1}{\mu} < \infty, \mathbb{V}[X_i] < \infty$ が成り立つとき、
- $\displaystyle \frac{M(t)}{t} \xrightarrow[t \to \infty]{a.s.} \mu$
- $\displaystyle \lim_{t \to \infty} \frac{m(t)}{t} = \mu$
となる。
証明は結構複雑なので後回しにしましょう。

式の形と直感的な意味が理解できれば十分です。
基本再生定理の直感的なイメージ
定理に登場する
- $\frac{M(t)}{t}$
- $\frac{m(t)}{t}$
の意味が理解できれば定理の意味はすんなり理解できます。
$\frac{M(t)}{t}$
そもそも $M(t)$ は、時刻 $t$ までの到着数を表しています。
その $M(t)$ を時間 $t$ を割っているので、$\frac{M(t)}{t}$ は到着数の時間平均です。つまり、
単位時間あたりどれくらい到着するか
を表しています。
単位時間とは、1秒や1分など時間を測る際の基準となる時間です。
$\displaystyle \frac{M(t)}{t} \xrightarrow[t \to \infty]{a.s.} \mu$
$\frac{M(t)}{t}$ が単位時間あたりの到着数を表すので、時間に関する極限を取った $\frac{M(t)}{t} \xrightarrow[t \to \infty]{a.s.}$ は
十分長い時間が経った時の単位時間あたりの到着数
を表しています。
下の画像を見るとイメージがつかみやすいと思います。
これが $\mu =\frac{1}{\mathbb{E}[X_n]}$ に収束するというのは、具体例を考えると分かりやすいです。
例えば、到着間隔の期待値が10秒($\mathbb{E}[X_n] = 10 \Rightarrow \mu = \frac{1}{10}$)だとしましょう。

到着間隔の期待値が10秒ということは、だいたい10秒に1回到着があることが見込まれるということです。
直感的に考えると、1秒あたりの到着数は $\frac{1}{10}$ となりそうですよね。
もちろん到着にはばらつきがあるので必ず1秒に $\frac{1}{10}$ 回到着するわけではありませんが、基本再生定理の
$$\displaystyle \frac{M(t)}{t} \xrightarrow[t \to \infty]{a.s.} \mu$$
は、十分に時間が経てば確かに1秒あたりの到着数は $\frac{1}{10}$ になるということを示しています。

つまり、直感通りの結果になるというのが基本再生定理①の主張なのです。
続いて、$\frac{m(t)}{t}$ についてです。
$\frac{m(t)}{t}$
$m(t) = \mathbb{E}[M(t)]$ なので、$m(t)$ は時刻 $t$ の時点でどれくらい到着していることが見込まれるかを表しています。
その $m(t)$ を時間 $t$ で割った $\frac{m(t)}{t}$ は、
単位時間あたりに見込まれる到着数
を表しています。

$\frac{M(t)}{t}$ と $\frac{m(t)}{t}$ の違いは、実際に観測した到着数か見込まれる到着数かです。
$\displaystyle \lim_{t \to \infty} \frac{m(t)}{t} = \mu$
$\frac{m(t)}{t}$ が単位時間あたりに見込まれる到着数を表すので、時間に関する極限を取った $\lim_{t \to \infty} \frac{m(t)}{t}$ は
十分長い時間が経った時の単位時間あたりの見込み到着数
を表しています。
これが $\mu =\frac{1}{\mathbb{E}[X_n]}$ に収束するので、
$$\frac{M(t)}{t} \xrightarrow[t \to \infty]{a.s.} \lim_{t \to \infty} \frac{m(t)}{t}$$
が成り立ちます。
これは、十分に長い時間が経つと
が一致することを表しています。

つまり、「見込み」と「実際」が一致するというのがこの定理の主張です!
基本再生定理のイメージはつかめたでしょうか?
以上で説明は終了です。ここからは証明になるので、興味がある方はじっくり読んでみましょう。
基本再生定理①の証明
定理①
$$\displaystyle \frac{M(t)}{t} \xrightarrow[n \to \infty]{a.s.} \mu$$
の証明には、大数の強法則という法則を使います。
大数の強法則
独立同分布の確率変数列 $\{X_n\}_{n \in \mathbb{Z}+}$ について、
が成り立つとき、
$$\frac{1}{n} \sum_{i=1}^n X_i \xrightarrow[n \to \infty]{a.s.} \mu$$
が成り立つ。

大数の強法則は、平均値が期待値に収束する確率が1ということを表しています。
これを踏まえて証明に入ります。
証明
\begin{eqnarray} \lim_{n \to \infty} \frac{Z_n}{n} &=& \lim_{n \to \infty} \frac{\sum_{i=1}^n X_i}{n} \\ &=& \lim_{n \to \infty} \frac{X_1 + \sum_{i=2}^n X_i}{n} \\ &=& \lim_{n \to \infty} \frac{X_1}{n} + \lim_{n \to \infty} \frac{\sum_{i=2}^n X_i}{n} \\ &=& \lim_{n \to \infty} \frac{X_1}{n} + \lim_{n \to \infty} \frac{n-1}{n} \frac{\sum_{i=2}^n X_i}{n-1} \\ &=& \lim_{n \to \infty} \frac{n-1}{n} \frac{\sum_{i=2}^n X_i}{n-1} \end{eqnarray}
定義より $\mathbb{E} [X_i] = \frac{1}{\mu}$ だから、大数の強法則より
\begin{eqnarray} \mathbb{P} \left ( \lim_{n \to \infty} \frac{\sum_{i=2}^n X_i}{n-1} = \frac{1}{\mu} \right ) &=& 1 \end{eqnarray}
よって、
\begin{eqnarray} \mathbb{P} \left(\lim_{n \to \infty} \frac{Z_n}{n} = \frac{1}{\mu} \right) &=& \mathbb{P} \left (\lim_{n \to \infty} \frac{n-1}{n} \frac{\sum_{i=2}^n X_i}{n-1} = \frac{1}{\mu} \right) \\ &=& 1 \end{eqnarray}
次に、$\lim_{t \to \infty} M(t) < \infty$ となる確率を考える。
$\lim_{t \to \infty} M(t)$ は限りなく長い時間が経った時点で到着した電車の本数だから、これが有限だと仮定すると、どこかで電車が到着しなくなることになる。
言い方を変えると、待ち時間が無限大になることになる。数式で書くと、
$$\exists n \in \mathbb{Z}, \quad X_n = \infty$$
しかし、これは $\mathbb{E} [X_n] < \infty$ に矛盾するので、
$$ M(t) \xrightarrow[t \to \infty]{a.s.} \infty$$
先ほどの「$\mathbb{P} \left(\lim_{n \to \infty} \frac{Z_n}{n} = \frac{1}{\mu} \right) = 1$」を利用すると、
$$\mathbb{P} \left(\lim_{t \to \infty} \frac{Z_{M(t)}}{M(t)} = \frac{1}{\mu} \right) = 1$$
さらに、
\begin{eqnarray} \frac{Z_{M(t)}}{Z_{M(t)+1}} &=& \frac{Z_{M(t)}}{Z_{M(t)}+X_{M(t)+1}} \\ &=& \frac{ \frac{Z_{M(t)}}{M(t)} }{ \frac{Z_{M(t)}}{M(t)} + \frac{X_{M(t)+1}}{M(t)} } \\ &\xrightarrow[t \to \infty]{a.s.}& \frac{ \frac{1}{\mu} }{ \frac{1}{\mu} + 0 } \\ &=& 1 \end{eqnarray}
ここで、$Z_{M(t)} \leq t < Z_{M(t)+1}$ より $\frac{Z_{M(t)}}{Z_{M(t)+1}} < \frac{Z_{M(t)}}{t} \leq 1$ なので、はさみうちの原理より
$$\frac{Z_{M(t)}}{t} \xrightarrow[t \to \infty]{a.s.} 1$$
以上より、
\begin{eqnarray} \frac{M(t)}{t} &=& \frac{Z_{M(t)}}{t} \frac{M(t)}{Z_{M(t)}} \\ &=& \frac{Z_{M(t)}}{t} \frac{1}{\frac{Z_{M(t)}}{M(t)}} \\ &\xrightarrow[t \to \infty]{a.s.}& 1 \frac{1}{\frac{1}{\mu}} \\ &=& \frac{1}{\mu} \end{eqnarray}
基本再生定理②の証明
定理②
$$\displaystyle \lim_{t \to \infty} \frac{m(t)}{t} = \mu$$
の証明には、
- 停止時刻
- ウォールドの方程式
というものを使います。
停止時刻(Stopping Time)
独立な確率変数列 $\{X_n\}_{n \in \mathbb{N}}$ に対して、整数値の確率変数 $N$ を考える。
事象 $N=n$ が時刻 $n$ 以降の確率変数列 $\{X_{n+1}, X_{n+2}, \cdots\}$ と独立のとき、$N$ を停止時刻という。

$\{X_n\}$ を何かのゲームの結果、$N$ をゲームをやめるタイミングとして考えるとイメージしやすいです。
$n$ 回目のプレイ後にゲームをやめる場合、そのゲームをやめるという決断をするにあたって $n$ 回目までのゲーム結果を考えることはありますが、$n+1$ 回目以降のゲーム結果を考えることはないですよね。
なぜなら $n+1$ 回目以降の結果はプレイしてみるまでわからないので、考慮に入れようがないからです。
このように、$n$ 回目までの情報には依存するかもしれないけど、
$n+1$ 回目以降の情報とはまったく関係ない
という確率変数が停止時刻です。
ウォールドの方程式
独立同分布な確率変数列 $\{X_n\}$ とその停止時刻 $N$ について、
ならば
$$\mathbb{E} \left[ \sum_{i=1}^N X_i \right] = \mathbb{E} [X_n] \mathbb{E} [N]$$
が成り立つ。

これは意味を捉えるよりも、式変形の道具として使うだけなので形だけ覚えれば大丈夫です。
ウォールドの方程式を使うと、次の性質が導かれます。
到着間隔 $\{X_n\}$ の期待値が $\mathbb{E} [X_n] = \frac{1}{\mu} < \infty$ を満たすなら、
$$\mathbb{E}[Z_{M(t)+1}] = \frac{m(t)+1}{\mu}$$
$\{Z_n\}$ は到着時刻で $Z_n = \sum_{i=1}^n X_i$ の関係があります。
まず、$M(t)+1$ が停止時刻であることを示す。
\begin{eqnarray} M(t) + 1 = n &\iff& M(t) = n \,-\, 1 \\ &\iff& \sum_{i=1}^{n-1} X_i \leq t \lt \sum_{i=1}^{n} X_i \end{eqnarray}
よって、$M(t)+1$ は $\{X_{n+1}, X_{n+2}, \cdots \}$ とは独立だから停止時刻である。
したがって、ウォールドの方程式が適用でき
\begin{eqnarray} \mathbb{E}[Z_{M(t)+1}] &=& \mathbb{E}\left[\sum_{i=1}^{M(t)+1} X_i \right] \\ &=& \mathbb{E}[X_n] \mathbb{E}[M(t)+1] \\ &=& \frac{1}{\mu} (m(t) +1) \end{eqnarray}
これを踏まえて証明に入りましょう。
証明
任意の時刻 $t$ において、
$$t < \sum_{i=1}^{M(t)+1} X_i$$
が成り立ち、また
$$\sum_{i=1}^{M(t)+1} X_i < t +N$$
となるような定数 $N$ が存在する。
$\forall n \in \{2, 3, \cdots\}, \mathbb{E} [X] < \infty$ なので、$X_n < \infty$ です。そのため、例えば $N = max\{X_n\} + 1$ のようにすれば OK です。
よって
\begin{eqnarray} t < \sum_{i=1}^{M(t)+1} < t + N &\iff& \mathbb{E}[t] < \mathbb{E} [\sum_{i=1}^{M(t)+1}] < \mathbb{E} [t+N]\\ &\iff& t < \frac{1}{\mu} (m(t)+1) < t+N\\ &\iff& \mu t \,-\, 1 < m(t) < \mu (t+N) \,-\, 1\\ &\iff& \mu \,-\, \frac{1}{t} < \frac{m(t)}{t} < \mu (1+ \frac{N}{t})\, -\, \frac{1}{t}\\ \end{eqnarray}
ここで
\begin{array}{1} \mu \,-\, \frac{1}{t} \xrightarrow[t \to \infty]{} \mu \\ \mu (1+ \frac{N}{t})\, -\, \frac{1}{t} \xrightarrow[t \to \infty]{} \mu \\ \end{array}
だから、はさみうちの原理より
$$\frac{m(t)}{t} \xrightarrow[t \to \infty]{} \mu$$

コメント