再生過程・再生関数とは？図と具体例でわかりやすく解説

どうも！初めましての方は初めまして、初心者のWebサイト勉強のとみーです！

確率論の中には、再生過程（Renewal Process）という確率過程を扱う再生理論と呼ばれる分野があります。

とみー

この再生理論は待ち行列理論に応用される重要な理論です。

そこで今回は、その基礎となる再生過程について解説します！

再生過程・再生関数とは？

再生過程をイメージしやすくするために、具体例を使って考えましょう。

条件・設定

電車の駅には１つ前の駅から電車が到着し、乗客を乗せて次の駅へ出発します。

とみー

そして、１本出発すると次の電車が到着します。

到着間隔 $\{X_n\}$

駅同士の間隔は一定なので、ある電車が出発してから次の電車が到着するまでの間隔は独立同分布と考えられます。

そのため、$n-1$ 本目の電車が到着してから $n$ 本目の電車が到着するまでの間隔を $X_n$ とすると、

$\{X_n{\}}_{n\ge 2}$ は独立同分布

です。

ここで、なぜ $n=1$ が含まれていないかというと、電車の本数を数え始めたタイミングが

など様々に異なり、電車同士の到着間隔として定義できないからです。

とみー

つまり、$X_1$ だけは別の確率分布に従います。

再生点：到着時刻 $\{Z_n\}$

到着間隔 $\{X_n\}$ を用いると、$n$ 本目の電車の到着時刻 $Z_n$ は

$$Z_n=\sum _{i=1}^n{X}_i$$

と表されます。

とみー

ちなみに、$Z_1,Z_2,\cdots$ は再生点と呼ばれ、区間 $[Z_1,Z_2],[Z_2,Z_3],\cdots$ はサイクルと呼ばれます。

再生過程

以上の記号を使って表される

を再生過程といいます。

これは、

を表しています。

再生関数

再生過程の期待値

を、再生関数といいます。

再生関数は、

を表しています。

参考 再生過程・再生関数、$\{X_n\}$ や $\{Z_n\}$ の確率分布については、こちらの記事で詳しく解説しています。

再生過程の確率分布と再生関数の関係を解説！－畳み込み積分

どうも！初めましての方は初めまして、初心者のWebサイト勉強のとみーです！ 前回 再生過程の再生関数は、到着間隔の確率分布を使って表すことができます。 とみー 今回は、そんな再生関数と到着間隔の確率分布の関係をまとめました！ 対象レベル 確...

www.beginner-blogger.com

再生過程で登場する用語

再生過程では、上で定義した再生点や再生関数以外にも次のような用語が登場します。

とみー

１つずつ見ていきましょう！

待ち時間・余命

待ち時間は次の式で定義されます。

待ち時間は、

です。

とみー

電車の到着というシステムでは待ち時間ですが、例えば機械の故障というシステムの場合は「機械が壊れるまでの時間＝余命」と言えます。

経過時間・年齢

経過時間は次の式で定義されます。

経過時間は、

です。

スプレッドと待ち時間・経過時間

スプレッドは次の式で定義されます。

スプレッドは、

です。

図から分かるように、

$$X(t)=X_{M(t)+1}$$

です。

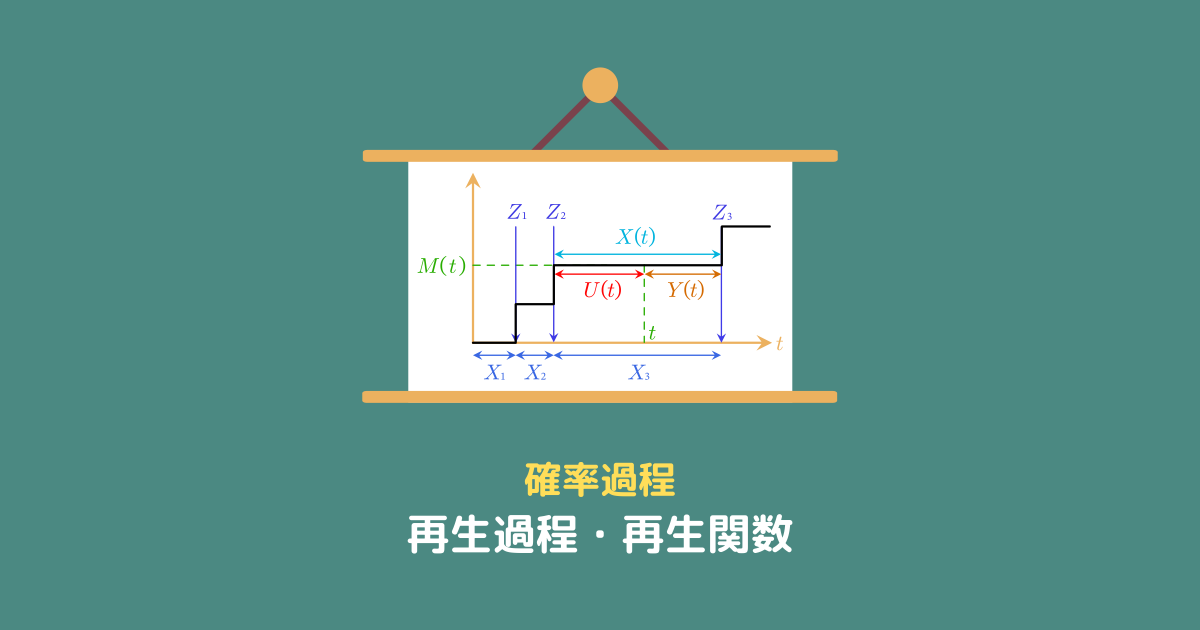
再生過程－まとめの図

今回は、再生過程をご紹介しました。

今回の内容をまとめると次の図のようになります。

とみー

ごちゃごちゃしてきたらこの図に立ち返って整理しましょう！

また、再生過程をひとことで言うと

を表す確率過程ということになります。