ポアソン過程をベルヌーイ試行で間引くとポアソン過程になる性質を証明する

どうも！初めましての方は初めまして、初心者のWebサイト勉強のとみーです！

ポアソン過程は、

ある時刻までに希少現象が発生した回数の総和

をモデル化できる確率過程で、待ち行列理論でよく用いられます。

参考ポアソン過程の基礎については、こちらでわかりやすくまとめています。

ポアソン過程とポアソンの極限定理をわかりやすく解説！

どうも！初めましての方は初めまして、初心者のWebサイト勉強のとみーです！待ち行列理論では、ポアソン過程と呼ばれる確率過程がよく登場します。確率過程は、簡単にいうと時刻

https://www.beginner-blogger.com/poisson-process/

, 1, \cdots, t, \cdots$ の確率変数を集...

ポアソン過程には、重要な性質がいくつかあります。

ポアソン過程に関連する重要事項

そして、ポアソン過程を扱う問題では、

ポアソン過程のイベントをランダムに２分割する

設定がしばしば登場します。

とみー

今回は、そのような設定でよく利用する定理を証明付きでわかりやすくまとめました！

対象レベル

確率の基本的な知識がある方（高校数学〜大学入門）

確率過程のおすすめ本

森北出版

入門確率過程

Amazonで見る楽天市場で見る Yahoo!ショッピングで見る

入門書ならこっち！

確率・統計理工系の数学入門コース　新装版

Amazonで見る楽天市場で見る Yahoo!ショッピングで見る

ポアソン過程のイベントをベルヌーイ試行で間引くとは
ポアソン過程をベルヌーイ試行で間引くとポアソン過程になる
まとめ

ポアソン過程のイベントをベルヌーイ試行で間引くとは

まず、話をわかりやすくするために設定を明らかにしておきましょう。

到着率 $λ$ のポアソン過程

具体例の設定

今回は、ポアソン過程として時刻 $t$ までに店に到着した客数 $Λ (t)$ を考えます。

とみー

ここでは客数としましたが、バスの到着や電話の着信など、ポアソン過程でモデル化できるものなら何でも構いません。

また、ポアソン過程の到着率を $λ$ とします。つまり、

$Λ (t) \sim P o i s (λ t)$

です。

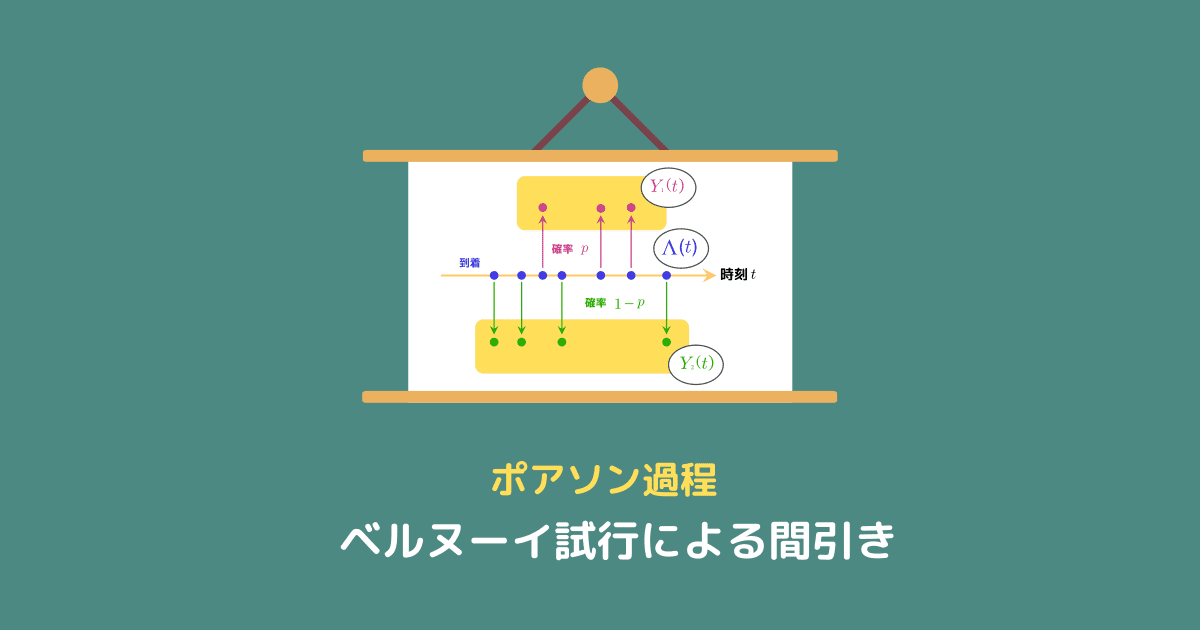
$i$ 番目の客の到着時刻を $Z_{i}$ とすると、次の図のようになります。

そして、このポアソン過程をベルヌーイ試行で間引くことを考えます。

ベルヌーイ試行による間引き

ベルヌーイ試行とは、

取り得る結果が２通り
どちらが発生する確率も一定

という試行です。

例えばコイントスは結果が「表」と「裏」の２通りだけで、表が出る確率、裏が出る確率はともに常に $\frac{1}{2}$ のベルヌーイ試行です。

そのほかにも

サイコロの目が３の倍数かどうか
５４枚のトランプの山から１枚引いた時に、それがジョーカーかどうか

といった試行もベルヌーイ試行となります。

とみー

確率が一定というのは、外的要因によらず何回試行を繰り返しても一定であることを意味します。

例えば「トランプの山から１枚引いた時に、それがジョーカーかどうか」を確認する試行は、トランプの山の枚数に依存するため、ベルヌーイ試行ではありません。

ベルヌーイ試行によるポアソン過程のイベントの間引き

ベルヌーイ試行が理解できたら、もとの問題の設定に戻りましょう。

今回は、時刻 $t$ までに到着した $Λ (t)$ 人の客のそれぞれを

確率 $p$ でグループ１
確率 $q = 1 - p$ でグループ２

というルールによってグループ分けすることを考えます。

つまり、パラメータ $p, q (= 1 - p)$ による $Λ (t)$ 回のベルヌーイ試行となります。

グループ１、グループ２という名前だと抽象的で理解しにくいですが、具体例として

グループ１：時刻 $t$ の時点で店に留まっている人のグループ
グループ２：時刻 $t$ の時点ですでに退店した人のグループ

のようなものが該当します。

とみー

当然この形にはまっていれば店内にいる人・退店した人というグループ分け以外でも適用できるため、かなり応用範囲が広い設定です。

ポアソン過程をベルヌーイ試行で間引くとポアソン過程になる

このようにしてポアソン過程を分割し、次のようになったとします。

時刻 $t$ の時点で店に留まっている人数： $Y_{1} (t)$
時刻 $t$ の時点で店に留まっている人数： $Y_{2} (t) = Λ (t) - Y_{1} (t)$

するとこのとき、次の定理が成り立ちます。

定理

$Y_{1} (t), Y_{2} (t)$ は互いに独立
$Y_{1} (t) \sim P o i s (λ t p)$
$Y_{2} (t) \sim P o i s (λ t q)$

２と３は、元のポアソン分布のパラメータに、ベルヌーイ試行の対応する確率をかけたパラメータを持つポアソン分布になることを表しています。

定理をわかりやすく言い換える

この定理を簡単にいえば、

ポアソン過程をベルヌーイ試行で間引いたものは、ポアソン過程になる

ということになります。

とみー

この定理を単体で使うというよりは、他の問題を解く最中に使うことが多いです。

導出にあたって必要な知識を整理しておきましょう。

専門性を活かした就活で差をつけよう！

確率や統計の専門性は理系の就活でかなり優位に働きます。

そのため、エンジニア就活特化のプラットフォームを使えば他では見られない高待遇な就職先が見つかります！

	特徴	リンク
UZUZ理系	内定率 86% 以上！ブラック企業徹底排除機械・電気電子・情報系は特に求人多数	【UZUZ】
エンジニア就活	未経験から即戦力まで幅広く対応 IT企業特化の企業研究・就活コラム企業から直接スカウトも！	【エンジニア就活】
レバテックルーキー	書類通過率 90% 以上プログラミング経験者限定のハイクラス求人新卒年収 500 万円以上の求人も！	レバテックルーキー

経験不足で大丈夫かな…という方はプログラミングスクールでスキルアップしておくとバッチリです。

	特徴	リンク
エンジニアズゲート	完全無料のプログラミングスクール！ 95% 超えの就職率専任のキャリアアドバイザーがサポート	エンジニアズゲート
TechAcademy	Web 制作・アプリ開発・AI など幅広いコース学割あり初心者からでも副業できるレベルのスキルが身に付く！	テックアカデミー無料体験

とみー

エンジニアズゲートは特に完全無料なので検討の余地ありです！

ベルヌーイ試行と二項分布

先ほど説明した通り、ベルヌーイ試行は「成功・失敗」のように２つの結果のうちのどちらかとなる試行です。

ベルヌーイ試行を $n$ 回繰り返したときに $k$ 回成功する確率は二項分布 $B (n, k)$ として知られており、確率質量関数は次のように表されます。

二項分布の確率質量関数

$_{n} C_{k} p^{k} (1 - p)^{(1 - k)}$

「成功する確率」という書き方をしましたが、問題設定に応じて「３の倍数が出る確率」といった具合に適宜読み替えて大丈夫です。

ポアソン分布の確率質量関数

こちらは復習になりますが、到着率 $λ$ の場合ポアソン分布のパラメータは $λ t$ なので、ポアソン分布の確率質量関数は以下の通りです。

ポアソン分布の確率質量関数

$P (Λ (t) = k) = \frac{(λ t)^{k} e^{- λ t}}{k!}$

ポアソン過程とポアソンの極限定理をわかりやすく解説！

https://www.beginner-blogger.com/poisson-process/

, 1, \cdots, t, \cdots$ の確率変数を集...

とみー

以上の知識で導出に取り掛かれます！

導出

$\begin{array}{rcl} P (Y_{1} (t) = i, Y_{2} (t) = j) & = & P (Y_{1} (t) = i, Y_{2} (t) = j | Λ (t) = i + j) P (Λ (t) = i + j) \\ = & P (Y_{1} (t) = i | Λ (t) = i + j) P (Λ (t) = i + j) \\ = & _{i + j} C_{i} p^{i} q^{j} \frac{(λ t)^{(i + j)} e^{- λ t}}{(i + j)!} \\ = & \frac{(i + j)!}{i! j!} p^{i} q^{j} \frac{(λ t)^{(i + j)} e^{- λ t}}{(i + j)!} \\ = & \frac{(λ t p)^{i}}{i!} \frac{(λ t q)^{j}}{j!} e^{- λ t} \\ = & \frac{(λ t p)^{i} e^{- λ t p}}{i!} \frac{(λ t q)^{j} e^{- λ t q}}{j!} \end{array}$

最後の２行は $p + q = 1$ であることを使って $e^{- λ t} = e^{- λ t (p + q)}$ として変形しています。

周辺化を行って同様の変形を行うと次のようになります。

$\begin{array}{rcl} P (Y_{1} (t) = i) & = & \sum_{j = 0}^{\infty} P (Y_{1} (t) = i | Λ (t) = i + j) P (Λ (t) = i + j) \\ = & \frac{(λ t p)^{i} e^{- λ t p}}{i!} \sum_{j = 0}^{\infty} \frac{(λ t q)^{j} e^{- λ t q}}{j!} \\ = & \frac{(λ t p)^{i} e^{- λ t p}}{i!} e^{λ t q} e^{- λ t q} \\ = & \frac{(λ t p)^{i} e^{- λ t p}}{i!} \end{array}$

赤字の部分はネイピア数のマクローリン展開です。

これを $P (Y_{2} (t) = j)$ に対して行うと

$\begin{array}{rcl} P (Y_{2} (t) = j) & = & \frac{(λ t q)^{i} e^{- λ t q}}{i!} \end{array}$

ここで、 $P (Y_{1} (t) = i)$ と $P (Y_{2} (t) = j)$ をよく見ると、

$\frac{(λ t p)^{i} e^{- λ t p}}{i!}$ ：パラメータ $λ t p$ のポアソン分布
$\frac{(λ t q)^{j} e^{- λ t q}}{j!}$ ：パラメータ $λ t q$ のポアソン分布

となっています。

つまり、

$Y_{1} (t)$ ：パラメータ $λ t p$ のポアソン分布
$Y_{2} (t)$ ：パラメータ $λ t q$ のポアソン分布

であることが示されました。

さらに最初の式に戻ると、最終行は「 $i を含む値 \times j を含む値$ 」なので、

$\begin{array}{rc} P (Y_{1} (t) = i, Y_{2} (t) = j) & = \frac{(λ t p)^{i} e^{- λ t p}}{i!} \frac{(λ t q)^{j} e^{- λ t q}}{j!} \\ = P (Y_{1} (t) = i) P (Y_{2} (t) = j) \end{array}$