どうも!初めましての方は初めまして、初心者のWebサイト勉強のとみーです!
ポアソン過程は、
ある時刻までに希少現象が発生した回数の総和
をモデル化できる確率過程で、待ち行列理論でよく用いられます。
参考 ポアソン過程の基礎については、こちらでわかりやすくまとめています。
そして、このポアソン過程は再生過程(Renewal Process)と呼ばれる確率過程と密接な関係にあります。
参考 再生過程については、こちらの記事でわかりやすくまとめています。
もっと具体的にいうと、
ポアソン過程は再生過程
という関係があります。

今回は、そんなポアソン過程と再生過程の関係について1つずつ順を追って理解できるように整理してみました!
確率の基本的な知識がある方(高校数学〜大学入門)
ポアソン過程の設定
まず、話をわかりやすくするために設定を明らかにしておきましょう。
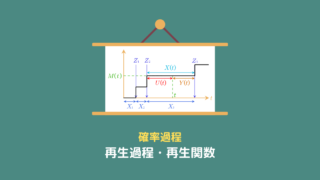
今回は、ポアソン過程として時刻 $t$ までに店に到着した客数 $\Lambda(t)$ を考えます。
$i$ 番目の客の到着時刻を $Z_i$ とすると、次の図のようになります。
このとき、$\Lambda (t)$ はポアソン過程なので、ポアソン分布 $Pois(\lambda t)$ に従います。
$\lambda$ は正のパラメータです。
つまり、
$\mathbb{P}(\Lambda (t) = i) = \displaystyle \frac{e^{-\lambda t} (\lambda t)^i }{i!}$
となります。

どこからこの式が出てきたのか、なぜ客の到着数がポアソン過程として表せるのかについては、こちらをご覧ください。
ポアソン過程の到着間隔を考える
再生過程は、
を表す確率過程です。

何を言っているかわからない…
という方は、こちらで再生過程の基本についてまとめているのでご覧ください。
ポアソン過程の話を再生過程の話に持っていくために、ここからは「到着時間」ではなく「到着間隔」を考えます。
$i\,-\,1$ 番目の到着と $i$ 番目の到着の間隔を $X_i$ とすると、次の図のようになります。
ポアソン過程が再生過程であることを確かめる

ここからが本題です!
ポアソン過程が再生過程であることを確かめるために、
到着間隔が独立同分布
であることを見ていきましょう。
独立同分布であることをチェックするためには、そもそも到着間隔がどういう確率分布に従うのかを知る必要があります。
- 確率分布が知りたい
- 累積分布関数 $\mathbb{P} (X_i \leq t)$ が分かればいい
- 余事象を取った $\mathbb{P} (X_i > t) $ でも良い
- $X_i > t$ がどういう状況か分かればOK

このように考えると、$X_i > t$ から出発するのが良さそうですね。
最初の到着 $X_1$ の確率分布を求める
まずは1番最初の到着 $X_1$ からいきましょう。
$X_1 > t$ はどういう状況か
$X_1 > t$ というのは、最初の到着が $t$ よりも後ということです。
言い換えると、時刻 $t$ の時点では誰も到着していない、つまり
$\Lambda (t) = 0$
と同値です。
$\mathbb{P} (X_1 > t)$ を求める
よって
$ \begin{eqnarray} \mathbb{P} (X_1 > t) &=& \mathbb{P} (\Lambda (t) = 0) \\ &=& e^{-\lambda t} \end{eqnarray} $
が成り立ちます。
累積分布関数 $\mathbb{P} (X_1 \leq t)$ を求める
上の結果の余事象を取ると、累積分布関数が求められます。
$ \begin{eqnarray} \mathbb{P} (X_1 \leq t) &=& 1 \;-\; \mathbb{P} (X_1 > t) \\ &=& 1 \;-\; e^{-\lambda t} \end{eqnarray} $
確率分布を求める
実は、$F_X (x) = 1 \;-\; e^{-\lambda x}$ は、$\lambda > 0$ をパラメータにもつ
指数分布 $\mathcal{E} (\lambda)$
の累積分布関数です。
厳密にいうと、指数分布 $\mathcal{E} (\lambda)$ に従う確率変数 $X$ の累積分布関数です。

ということは、上の結果から $X_1$ は $\mathcal{E}(\lambda)$ に従うことがわかります!
式で書くと
$X_1 \sim \mathcal{E} (\lambda)$
ですね。
2回目の到着 $X_2$ の確率分布を求める
次に2回目の到着 $X_2$ について考えましょう。
$X_2 > t$ はどういう状況か
$X_2 > t$ というのは、2回目の到着間隔が $t$ よりも後ということです。

先ほどとは異なり、今回は最初の到着がいつかによっていろんなパターンが考えられます。
例えば、$t = 5$ のとき
などが考えられ、実際にはもっとたくさんのケースがあります。
これを一般化すると、最初の到着時刻を $x$ としたときに、
$\mathbb{P} (X_2 > t \cap X_1 = x)$
となるケースがたくさんあるということです。
つまり、これをすべての $x$ について足し合わせれば $\mathbb{P} (X_2 > t)$ が求められます。
$\mathbb{P} (X_2 > t)$ を求める
ベイズの定理を使うと、以上の話は次のような積分を使って表せます。
$ \begin{eqnarray} \mathbb{P} (X_2 > t) &=& \int_0^\infty \mathbb{P} (X_2 > t \cap X_1 = x) dx \\ &=& \int_0^\infty \color{red} \mathbb{P} (X_2 > t \,|\, X_1 = x) \color{black} f_{X_1} (x) dx \end{eqnarray} $
$f_{X_1}$ は $X_1$ の確率密度関数です。
すでに $X_1 \sim \mathcal{E} (\lambda)$ であることがわかっているので、$f_{X_1} (x) = \lambda e^{- \lambda x}$ となります。
この式の中でわからないのは、$\mathbb{P} (X_2 > t \,|\, X_1 = x)$ ですね。

よって、次はこれを求めましょう。
$X_2 > t \,|\, X_1 = x$ はどういう状況か
$X_2 > t \,|\, X_1 = x$ は、
ことを表します。

先ほどの図をもう1回見てみましょう。
つまり、時間 $(x, x +t]$ での到着数は0、数式で書くと
$\Lambda (x+t) \; – \; \Lambda (x) = 0$
です。
$\mathbb{P} (X_2 > t \,|\, X_1 = x)$ を求める
ポアソン過程の定常増分性から、$\Lambda (x+t) \; – \; \Lambda (x)$ は $\Lambda (t)$ と同じ確率分布 $Pois(\lambda t)$ に従います。
よって
$ \begin{eqnarray} \mathbb{P} (X_2 > t \,|\, X_1 = x) &=& \mathbb{P} (\Lambda (x+t) \; – \; \Lambda (x) = 0 \,|\, X_1 = x) \\ &=& \mathbb{P} (\Lambda (t) = 0 \,|\, X_1 = x) \\ &=& \mathbb{P} (\Lambda (t) = 0) \\ &=& \color{red} e^{-\lambda t} \end{eqnarray} $
となります。
$\mathbb{P} (X_2 > t)$ が求められる
以上を踏まえると、
$ \begin{eqnarray} \mathbb{P} (X_2 > t) &=& \int_0^\infty \color{red} e^{-\lambda t}\color{black} f_{X_1} (x) dx \\ &=& e^{-\lambda t} \int_0^\infty f_{X_1} (x) dx \\ &=& e^{-\lambda t} \end{eqnarray} $
ここで重要なのは $x$ (最初の到着時刻)が式変形の結果消えたということです。
これは
$X_1$ と $X_2$ が互いに独立
であることを意味します。
確率分布を求める
上の結果の余事象を取ると、累積分布関数が求められます。
$ \begin{eqnarray} \mathbb{P} (X_2 \leq t) &=& 1 \;-\; \mathbb{P} (X_2 > t) \\ &=& 1 \;-\; e^{-\lambda t} \end{eqnarray} $
これは先ほどとまったく同じ指数分布 $\mathcal{E} (\lambda)$ の累積分布関数なので
$X_2 \sim \mathcal{E} (\lambda)$
です。
すべての到着間隔は指数分布 $\mathcal{E} (\lambda)$ に従う
以上を再帰的に繰り返すと、到着間隔 $\{X_i\}$ は
ということがわかります。
つまり、
到着間隔が独立同分布
であることが導かれました!

最後に再生過程の話としてまとめましょう!
ポアソン過程は到着間隔が指数分布に従う再生過程
ポアソン過程はもともと時刻 $t$ までの到着数を表していたので、上の結果を合わせると
という再生過程の定義を満たします。
さらに、到着間隔は
指数分布 $\mathcal{E} (\lambda)$
に従うということも導かれました。
以上より、
ポアソン過程は到着間隔が指数分布に従う再生過程
であることが結論付けられます。

お疲れさまでした!




コメント