どうも!初めましての方は初めまして、初心者のWebサイト勉強のとみーです!
再生過程の再生関数は、到着間隔の確率分布を使って表すことができます。

今回は、そんな再生関数と到着間隔の確率分布の関係をまとめました!
確率の基本的な知識がある方(高校数学〜大学入門)
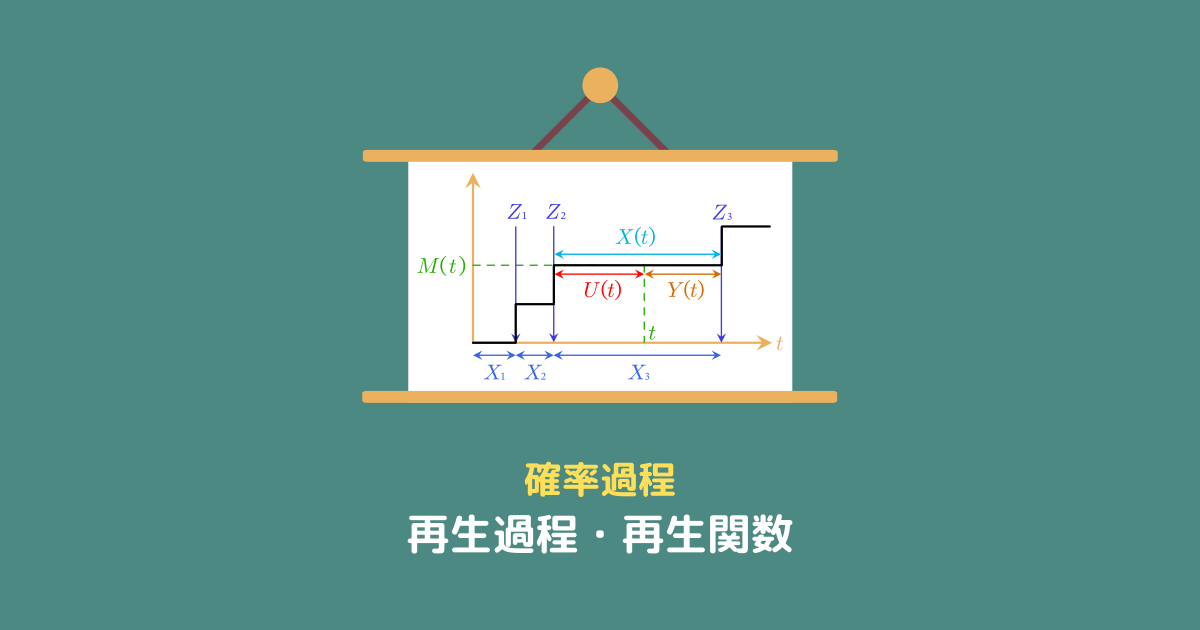
再生過程の設定
イメージをしやすくするために、前回の設定を引き続き使います。
忙しい方のために簡単にまとめると、電車の到着を題材として
という風に変数を置きます。
到着間隔 $\{X_n\}$ の確率分布
駅同士の間隔は一定なので、ある電車が出発してから次の電車が到着するまでの間隔は独立同分布です:
$\{X_n\}_{\color{red}n \geq 2 \color{black}}$ は独立同分布
そこで、対応する累積分布関数を
$$\forall n \in \{\color{red}2\color{black}, 3, \cdots\}, \quad F(t) = \mathbb{P} (X_n \leq t)$$
とします。
ただし、電車の本数を数え始めたタイミングは
など様々に異なるので、$n=1$ だけは例外です。
そのため、$X_1$ の累積分布関数は $F$ とは違う文字を使って
$$A(t) = \mathbb{P} (X_1 \leq t)$$
と表します。

$X_1$ と $X_2, X_3, \cdots$ は確率分布が異なりますが、独立です。
到着時刻(再生点)$\{Z_n\} $ の確率分布
到着間隔 $\{X_n\}$ と到着時刻 $Z_n$ の間には、
$$Z_n = \sum_{i=1}^{n} X_i$$
という関係があります。
そのため $\{X_n\}$ の確率分布を使うと、 $Z_n$ の確率分布を求めることができます。

$\{X_n\}$ が離散の場合と連続の場合で少し対応が異なります。
まず、方針を立てやすくするために $Z_2$ の確率分布を求めましょう。
$Z_1 = X_1$ なので $Z_1$ の確率分布は $X_1$ の確率分布と同じです。
$$\mathbb{P} (Z_1 \leq t) = A(t)$$
$\{X_n\}$ が離散の場合
$X_1$ の確率質量関数を
$$a[k] =\mathbb{P} (X_1 = k)$$
$X_2, X_3, \cdots$ の確率質量関数を
$$\forall n \in \{2, 3, \cdots\}, \quad f[k] =\mathbb{P} (X_n = k)$$
と置きます。
確率質量関数 $\mathbb{P} (Z_2 = k)$
$\{X_n\} $ が離散のとき、$Z_2$ の確率質量関数は
$$\mathbb{P} (Z_2 = k) = \sum_{i=0}^{k} a[k-i] f[i] = a * f [k]$$
となります。
記号「$*$」は畳み込み積分を表します。
$$Z_2 = k \iff X_1 + X_2 = k$$
$X_1 + X_2 = k$ となるのは、
$$(X_1, X_2) = (0, k), (1, k-1), \cdots, (k-1, 1), (k, 0)$$
のときで、$X_1$ と $X_2$ は独立だから
$$\mathbb{P} (X_1 = k \,-\, i, X_2 = i) = \mathbb{P} (X_1 = k \,-\, i) \mathbb{P}(X_2 = i)$$
と分離できる。よって
\begin{eqnarray} \mathbb{P} (Z_2 = k) &=& \sum_{i=0}^{k} \mathbb{P} (X_1 = k-i, X_2 = i) \\ &=& \sum_{i=0}^{k} \mathbb{P} (X_1 = k \,-\, i) \mathbb{P}(X_2 = i) \\ &=& \sum_{i=0}^{k} a[k-i] f[i] \\ &=& a * f [k] \end{eqnarray}
累積分布関数 $\mathbb{P} (Z_2 \leq k)$
一方で、$Z_2$ の累積分布関数は
$$\mathbb{P} (Z_2 \leq k) = \sum_{i=0}^{k} A(k-i) f[i] = A \circledast F (k)$$
です。
記号「$\circledast$」は、確率質量関数を持つ任意の累積分布関数 $B(k), C(k)$ について
\begin{eqnarray} B \circledast C (k) &=& \sum_{i=0}^k B(k-i) C'(i) \\ &=& \sum_{i=0}^k B'(i) C(k-i) \end{eqnarray}
となる演算子です(スティルチェス畳み込みと呼ばれます)。
$$Z_2 = X_1 + X_2 \leq k$$
となるのは、$X_2$ を $X_2 = i$ と固定すると $X_1 \leq k \, -\, i$ のときである。
よって
\begin{eqnarray} \mathbb{P} (Z_2 \leq k) &=& \sum_{i=0}^k \mathbb{P} (X_1 \leq k \,-\, i, X_2 = i) \\ &=& \sum_{i=0}^k \mathbb{P} (X_1 \leq k \,-\, i) \mathbb{P} (X_2 = i) \\ &=& \sum_{i=0}^k A(k-i) f[i] \\ &=& \sum_{i=0}^k A(k-i) F'(i) \\ &=& A \circledast F (k) \end{eqnarray}
$\{X_n\}$ が連続の場合
$X_1$ の確率密度関数を
$$a(t) = \frac{d}{dt} \mathbb{P} (X_1 \leq t) = \frac{d}{dt} A(t)$$
$X_2, X_3, \cdots$ の確率密度関数を
$$\forall n \in \{2, 3, \cdots\}, \quad f(t) =\frac{d}{dt}\mathbb{P} (X_n \leq t) = \frac{d}{dt} F(t)$$
とします。
確率密度関数 $f_{Z_2} (t)$
$\{X_n\} $ が連続のとき、$Z_2$ の確率密度関数は
\begin{eqnarray} f_{Z_2}(t) &=& \frac{d}{dt} \mathbb{P} (Z_2 \leq t) \\ &=& \int_0^t a(t-u) f(u) du \\ &=& a * f (k) \end{eqnarray}
となります。
$$Z_2 = t \iff X_1 + X_2 = t$$
離散の場合と同様に考えると
\begin{eqnarray} \frac{d}{dt} \mathbb{P} (Z_2 \leq t) &=& \int_{0}^{t} \mathbb{P} (X_1 = t-u, X_2 = u)du \\ &=& \int_{0}^{t} \mathbb{P} (X_1 = t \,-\, u) \mathbb{P}(X_2 = u)du \\ &=& \int_{0}^{t} a(t-u) f(u)du \\ &=& a * f (t) \end{eqnarray}
累積分布関数 $\mathbb{P} (Z_2 \leq t)$
また、累積分布関数は
$$\mathbb{P} (Z_2 \leq k) = \int_{0}^{t} A(k-u) f(u) du = A \circledast F (t)$$
です。
記号「$\circledast$」は、確率密度関数を持つ任意の累積分布関数 $B(k), C(k)$ について
\begin{eqnarray} B \circledast C (k) &=& \int_{0}^t B(k-u) C'(u) du \\ &=& \int_{0}^t B'(u) C(k-u) du \end{eqnarray}
となる演算子です(スティルチェス畳み込みと呼ばれます)。

先ほど定義したスティルチェス畳み込みの連続バージョンです。
離散のときと同様に、
$$Z_2 = X_1 + X_2 \leq k$$
となるのは、$X_2$ を $X_2 = i$ と固定すると $X_1 \leq k \, -\, i$ のときである。
よって
\begin{eqnarray} \mathbb{P} (Z_2 \leq t) &=& \int_0^t \mathbb{P} (X_1 \leq t \,-\, u, X_2 = u) du\\ &=& \int_0^t \mathbb{P} (X_1 \leq k \,-\, u) \mathbb{P} (X_2 = u)du \\ &=& \int_0^t A(k-u) f(u) du\\ &=& \int_0^t A(k-u) F'(u) du\\ &=& A \circledast F (t) \end{eqnarray}
$\{Z_n\}$ の確率分布
以上をまとめると、$\{X_n\}$ が離散の場合も連続の場合も
と表せます。
これを使うと、$Z_3$ では
\begin{eqnarray} \mathbb{P} (Z_3 \leq t ) &=& \mathbb{P} (Z_2 + X_3 \leq t) \\ &=& (A \circledast F) \circledast F (t) \\ &=& A \circledast F \circledast F (t) \end{eqnarray}
となって、$F$ が2回現れます。

同様に、$Z_n$ になると $F$ が $n-1$ 回現れることになります。
そこで、「$\circledast$」による $n$ 重の畳み込みを $F^{(n)}$ とすると
$$\mathbb{P} (Z_n \leq t) = A \circledast F^{(n-1)} (t)$$
となります。
$F^{(n+1)} = F^{(n)} \circledast F(t) = \underbrace{F \circledast \cdots \circledast F}_{n+1 \mbox{個}} (t)$ です。
この記法を使うと $n=1$ のとき $\mathbb{P} (Z_1 \leq t) = A \circledast F^{(0)} (t)$ になるので、先ほどの結果と合わせるために特別に
$$F^{(0)} = \mathbb{I}_{\mathbb{R}_+} (t) $$
とします。
$\mathbb{I}_A (t)$ は $t \in A$ のとき1、それ以外は0となる指示関数です。
再生関数と確率分布関数の関係
ここまでの内容を使うと、再生関数と確率分布関数の関係式を導くことができます。
そのために、まず再生過程 $M(t)$ について考えます。
再生過程 $M(t)$ と指示関数 $\mathbb{I}_{\{Z_i \leq t\}} (Z_i)$
任意の $i \in \mathbb{Z}$ について、次のような指示関数を考えます。
\begin{eqnarray} \mathbb{I}_{\{ Z_i \leq t \}} (Z_i) = \left \{ \begin{array}{1} 1 \quad (Z_i \leq t) \\ 0 \quad (Z_i \gt t) \end{array} \right . \end{eqnarray}
これは、
時刻 $t$ の時点で電車 $i$ が到着しているかどうかを判定
する関数です。
これを用いると、時刻 $t$ までに到着した電車の本数を表す $M(t)$ は、
$$M(t) = \sum_{i=1}^\infty \mathbb{I}_{\{Z_i \leq t\}} (Z_i)$$
と書けます。
再生関数 $m(t)$ と確率分布 $A(t), F(t)$
時刻 $t$ までに到着する電車の本数の期待値である再生関数 $m(t)$ は、上の指示関数を使うと
$$m(t) = \sum_{i=1}^\infty A \circledast F^{(i-1)} (t)$$
であることが導けます。
\begin{eqnarray} m(t) &=& \mathbb{E}[M(t)] \\ &=& \mathbb{E} \left[ \sum_{i=1}^\infty \mathbb{I}_{\{Z_i \leq t\}} (Z_i)\right] \\ &=& \sum_{i=1}^\infty \mathbb{E} \left[ \mathbb{I}_{\{Z_i \leq t\}} (Z_i)\right] \\ &=& \sum_{i=1}^\infty \mathbb{P} (Z_i \leq t) \\ &=& \sum_{i=1}^\infty A \circledast F^{(i-1)} (t) \end{eqnarray}
まとめ
今回は、再生過程の確率分布や再生関数について数学的な観点から深掘りをしました。

たくさん式が出てきたので、最後に重要なものをまとめておきましょう。

コメント