どうも!初めましての方は初めまして、初心者のWebサイト勉強のとみーです!
みなさんは、

自分が並ぶレジはいつも他のレジよりも待ち時間が長い気がする…
とか

なぜか混んでいる電車にばっか乗る気がする…
と感じたこと、ありませんか?
実は、
自分の待ち時間は平均よりも長くなる
というのは気のせいではなく、数学的に証明することができます。

そこで今回は、再生過程を用いてその仕組みを明らかにしていこうと思います!
確率の基本的な知識がある方(高校数学〜大学入門)
スプレッドを考えるための再生過程
まずは、問題の設定を明らかにしておきましょう。
条件・設定
ここでは電車の到着を例に考え、以下のように変数を設定します。
参考 再生過程の基本や電車の題材の詳しい説明は、こちらの記事をご覧ください。
スプレッド $X(t)$
スプレッドは、
$$X(t) = X_{M(t) + 1}$$
で表される変数です。
スプレッドは時刻 $t$ を含む到着間隔の長さを表しますが、分かりやすくいうと
時刻 $t$ に到着した客が観測する到着間隔
です。

そのため、$X(t)$ の確率分布がわかればどの到着間隔に遭遇しやすいかが分かります!
そこで、
$$\mathbb{P} (X(t) \leq x)$$
($x$ は任意の定数)を求めることが目標になります。
しかし、これを求めるにはテクニックが必要なので、一旦次のような再生報酬過程を考えます。
スプレッドを考えるための再生報酬過程
報酬の導入
求めたいのは
$$\mathbb{P} (X(t) \leq x)$$
なので、次のような報酬を考えます。
\begin{eqnarray} \mathbb{I}_{\{ X(t) \leq x \}} (t) = \left \{ \begin{array}{l} 1 \quad \cdots \quad X(t) \leq x \\ 0 \quad \cdots \quad X(t) > x \end{array} \right. \end{eqnarray}
これは、スプレッドが $x$ 以下となるような時刻 $t$ に客が到着できたら+1の報酬がもらえることを表しています。

言い換えると、$x$ 未満の長さの区間で+1の報酬が発生します。
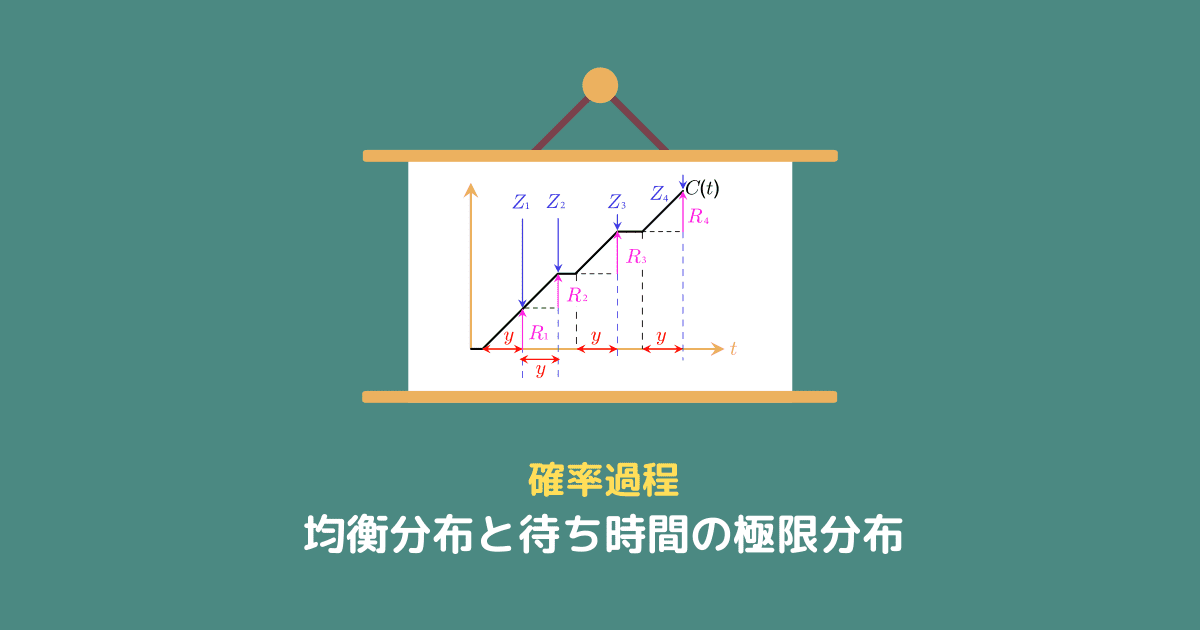
累積報酬 $C(t)$(再生報酬過程)
報酬 $\mathbb{I}_{\{X(t) \leq x\}}$ の表現を使うと、再生報酬過程(累積報酬)は次のように表されます。
$$C(t) = \int_0^t \mathbb{I}_{\{X(u) \leq x \}}du$$

時刻 $t$ と紛らわしいので、積分変数は $u$ としています。
$X(t) \leq x$ のときに報酬が1発生するので、累積報酬の傾きは1になります。

電車の到着時刻 $\{Z_n\}$ とは関係なく報酬が変化するので、これは部分報酬モデルです。
ちなみに、この $C(t)$ は $X(t) \leq x$ となる時間の総和、つまり
時刻 $t$ までの長さ $x$ 以下の到着間隔の総和
を表しています。
再生報酬関数 $c(t)$
再生報酬過程において、$c(t) = \mathbb{E} [C(t)]$ を再生報酬関数といいます。
今回の例では、
時刻 $t$ までに長さ $x$ 以下の到着間隔がどれくらいあると見込めるか
を表します。
$C(t) = \int_0^t \mathbb{I}_{\{ X(t)\leq x \}} (t) dt$ を代入して計算を行うと
$$c(t) = \int_0^t \mathbb{P} (X(u) \leq x) du$$
が得られます。

時刻 $t$ と紛らわしいので、ここでも積分変数は $u$ としています。
\begin{eqnarray} c(t) &=& \mathbb{E}[C(t)] \\ &=& \mathbb{E} \left [\int_0^t \mathbb{I}_{\{ X(u)\leq x \}} (u) du \right] \\ &=& \int_0^t \mathbb{E} [\mathbb{I}_{\{ X(u)\leq x \}} (u)] du \end{eqnarray}
ここで、$\mathbb{I}_{ \{ X(u) \leq x \} }$ は
なので、
\begin{eqnarray} \mathbb{E} [\mathbb{I}_{\{ X(u)\leq x \}} (u)] &=& 1 \cdot \mathbb{P} (X(u) \leq x) + 0 \cdot \mathbb{P} (X(u) > x) \\ &=& \mathbb{P} (X(u) \leq x) \end{eqnarray}
である。
よって
$$c(t) = \int_0^t \mathbb{P} (X(u) \leq x) du$$
部分報酬 $\{R_n\}$
部分報酬モデルの考え方にしたがって、時刻 $Z_n$ の累積報酬と時刻 $Z_{n-1}$ の累積報酬の差を部分報酬 $R_n$ とすると、
\begin{eqnarray} \forall n \in \mathbb{N}, \quad R_n = \left \{ \begin{array}{l} X_n \quad \cdots \quad X_n \leq x \\ 0 \quad \cdots \quad X_n > x \end{array} \right. \end{eqnarray}
となります。
再生報酬定理
ここまでで再生報酬過程が定義できたので、再生報酬定理を適用します。
すべての自然数 $n$ に対し、$\mathbb{E}[X_n] = \frac{1}{\mu} < \infty, \mathbb{V}[X_n] < \infty$、$\mathbb{E}[R_n] < \infty$ が成り立つとき、
$$\displaystyle \lim_{t \to \infty} \frac{c(t)}{t} = \mu \mathbb{E}[R_n]$$
となる。
参考 再生報酬定理については、こちらの記事で解説しています。

途中の式変形で登場するので、部分報酬の期待値だけ最初に確認しておきましょう。
部分報酬 $\{R_n\}$ の期待値 $\mathbb{E}[R_n]$
計算を行うと、$\{R_n\}$ の期待値は
$$\mathbb{E}[R_n] = xF_X(x) \; – \; \int_0^x F_X(u) du$$
であることが求められます。
部分積分を使うと
\begin{eqnarray} \int_0^\infty \mathbb{P}(R_n > u) du &=& \left [ u \mathbb{P}(R_n > u) \right ]_0^\infty \; – \int_0^\infty u \frac{\partial}{\partial u} \mathbb{P} (R_n > u) du \\ &=& 0 \; – \int_0^\infty u \frac{\partial}{\partial u} (1 \; – \; \mathbb{P} (R_n \leq u)) du \\ &=& – \int_0^\infty u \frac{\partial}{\partial u} (1 \; – \; F_R(u)) du \\ &=& – \int_0^\infty u (- f_R(u)) du \\ &=& \int_0^\infty u f_R (u) du \\ &=& \mathbb{E}[R_n] \end{eqnarray}
となる。
定義より $R_n \leq x$ なので、
\begin{eqnarray} \int_0^\infty \mathbb{P}(R_n > u) du &=& \int_0^x \mathbb{P}(R_n > u) du \end{eqnarray}
$0 < u < x$ のとき、
$$R_n > u \iff u < X_n \leq x$$
だから
\begin{eqnarray} \int_0^x \mathbb{P}(R_n > u) dx &=& \int_0^x \mathbb{P}(u < X_n \leq x) du \\ &=& \int_0^x (F_X(x) \,-\, F_X(u))du \\ &=& xF_X(x) \,-\, \int_0^x F_X(u) du \end{eqnarray}
再生報酬定理の適用
上で求めた $c(t)$ の表現を使うと、
$$\frac{c(t)}{t} = \frac{1}{t} \int_0^t \mathbb{P} (X(u) \leq x) du$$
なので、再生報酬定理を適用すると
$$\lim_{t \to \infty} \frac{1}{t} \int_0^t \mathbb{P} (X(u) \leq x) du = \mu \left (xF_X(x) \; – \; \int_0^x F_X(u) du \right)$$
となります。

これは後で式変形のために使うので、どういう意味かは置いておきましょう。
スプレッドの分布-客の到着が一様分布
さて、ここまでの話は客の到着時間に関して何も仮定していませんでした。

要するに、到着時間がどんな確率分布にしたがっていても成り立ちます。
ここからは、話をさらに深めていくために客が時刻 $0$ から $t$ の間でランダムに到着するとしましょう。
つまり、客の到着時間を $U$ としたときに、
$U$ は一様分布 $\mathcal{U}_{[0,t]}$ にしたがう
と仮定します。
このとき、確率密度関数は
\begin{eqnarray} f_U(u) = \left\{ \begin{array}{l} \frac{1}{t} \quad \cdots \quad u \in [0, t]\\ 0 \quad \cdots \quad u \notin [0, t] \end{array} \right. \end{eqnarray}
です。
スプレッドの確率分布
客の到着時間が一様分布にしたがうとき、スプレッドの累積分布関数は
$$\mathbb{P} (X(U) \leq x) = \int_0^\infty \mathbb{P} (X(u) \leq x) f_U(u) du$$
です。

これは累積分布関数を確率密度関数で表しただけです。
確率密度関数 $f_U$ を代入すると
$$\mathbb{P} (X(U) \leq x) = \frac{1}{t} \int_0^t \mathbb{P} (X(u) \leq x) du$$
となります。

これは先ほど上で見た $\frac{c(t)}{t}$ に他なりません!
スプレッドの極限分布
$\mathbb{P} (X(U) \leq x)$ と $\frac{c(t)}{t}$ が同じということは、先ほどの再生報酬定理の結果が使えるので
$$\lim_{t \to \infty} \mathbb{P} (X(U) \leq x) = \mu \left (xF_X(x) \; – \; \int_0^x F_X(u) du \right)$$
が成り立ちます。
この式の右辺は $x$ についての関数と見ることができるので、ここで
$$F_s(x) = \mu \left (xF_X(x) \; – \; \int_0^x F_X(u) du \right)$$
としましょう。
すると、$F_s(y)$ は
$x$ についての累積分布関数
になっています。
$F_s$ が累積分布関数であることを示すためには、
の2つを確かめればOKです。
まず、$x_1 < x_2$ とすると、
\begin{eqnarray} F_s (x_2) \;-\; F_s (x_1) &=& \mu \left (x_2 F_X (x_2) \; – \; \int_0^{x_2} F_X(u) du \right) \;-\; \mu \left (x_1 F_X (x_1) \; – \; \int_0^{x_1} F_X(u) du \right) \\ &=& \mu \left ( x_2F_X(x_2) \;-\; x_1 F_X(x_1) \; – \; \int_0^{x_1} F_X(u) du \;-\; \int_{x_1}^{x_2} F_X(u) du + \int_0^{x_1} F_X(u) du \right ) \\ &=& \mu \left ( x_2F_X(x_2) \;-\; x_1 F_X(x_1) \;-\; \int_{x_1}^{x_2} F_X(u) du \right ) \\ &=& \mu \left ( \left [u F_X(u) \right]_{x_1}^{x_2} \;-\; \int_{x_1}^{x_2} F_X(u) du \right ) \\ &=& \mu \left ( \int_{x_1}^{x_2} (F_X(u) + uf_X(u))du \;-\; \int_{x_1}^{x_2} F_X(u) du \right ) \\ &=& \mu \int_{x_1}^{x_2} u f_X(u) du \\ &>& 0 \end{eqnarray}
よって、$F_x$ は非減少。
また、$x_1 = 0, x_2 = \infty$ とすると、
\begin{eqnarray} F_s (\infty) \;-\; F_s (0) &=& \mu \int_{0}^{\infty} u f_X(u) du \\ \iff F_s (\infty) &=& \mu \int_{0}^{\infty} u f_X(u) du \\ &=& \frac{1}{\mathbb{E}[X_n]} \mathbb{E}[X_n] du \\ &=& 1 \end{eqnarray}
なので、$\lim_{x \to \infty} F_s(x) = 1$。

よって、スプレッドの極限分布は次のようになります。
ここまでで、必要な式はすべて揃いました。

それでは解釈をしていきましょう!
インスペクションパラドックス
スプレッドの極限分布の確率密度関数
$$f_s(x) = \mu x f_X(x)$$
に注目すると、
$f_s$ は $x$ に比例する
ことが分かります。

そして、$f_s(x)$ はランダムに到着した客が観測する到着間隔が $x$ となる確率です。
直感的には
客はランダムに到着するので観測される到着間隔もランダムになるはず
と思われますが、この結果が示しているのは
到着間隔が長ければ長いほど遭遇しやすい
ということです。
直感に反するこの現象は、インスペクションパラドックスと呼ばれます。

本来ならランダムである到着間隔のうち、長間隔の部分を優先的に選んでしまうという意味で、サンプリングにバイアスがかかるとも言われます。
まとめ

今回は、再生過程に関連するインスペクションパラドックスについて解説しました。
今回は
としましたが、これを
として同じように議論をすると、
混んでいるバスほど遭遇しやすい
という結論が導かれます。


コメント