どうも!初めましての方は初めまして、初心者のWebサイト勉強のとみーです!
確率論の1分野である再生理論で登場する再生過程は、シンプルで分析しやすいものの、シンプルすぎて逆に応用が効きにくいという問題があります。

そこで、再生過程を拡張した再生報酬過程というものが代わりに使われることがあります。
そこで今回は、その再生報酬過程について解説します!
参考 再生過程の基本については、こちらの記事をご覧ください。
確率の基本的な知識がある方(高校数学〜大学入門)
再生過程の問題点
イメージをしやすくするために、電車の到着を題材として
のように変数を置きましょう。
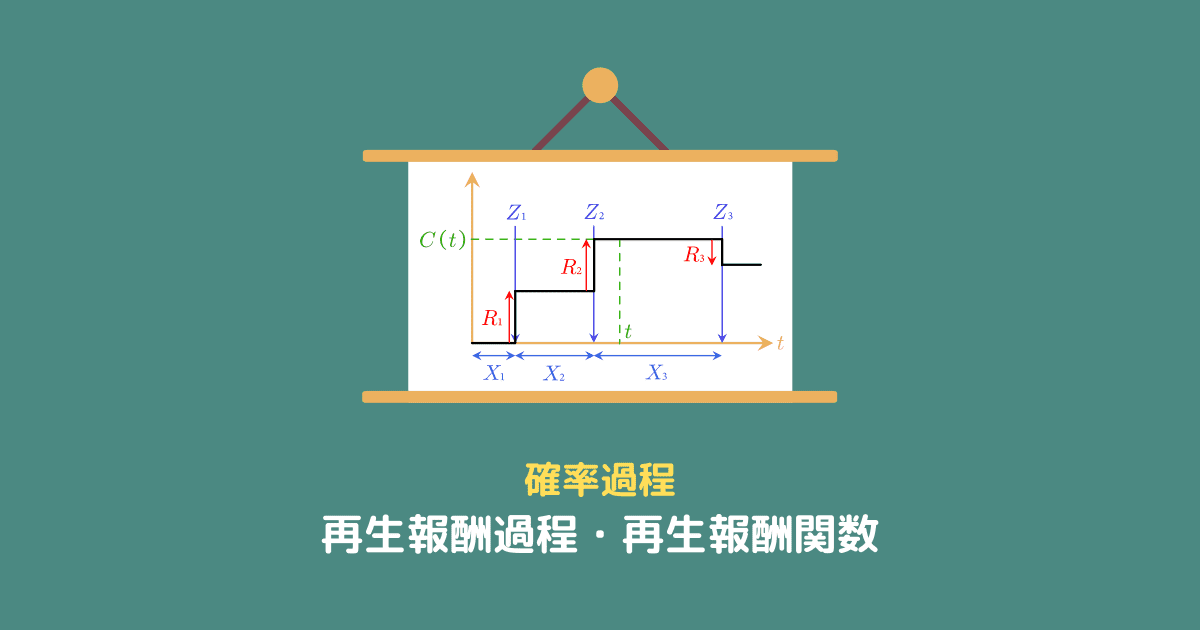
図にすると、次のような感じです。

時刻を測り始めてから $X_1$ だけ経った時刻 $Z_1$ に最初の電車が到着し、さらに $X_2$ だけ経った時刻 $Z_2$ で2番目の電車が到着するといったイメージです。
このモデルは非常にシンプルで電車の到着でカウントを増やしていくため、
$M(t)$ は自然数値
しか取ることができません。
また、電車1台の到着で1増えるような仕組みなので、
増え幅も1で固定
されています。
さらに、このモデルでは
$M(t)$ が減ることはない
ので、応用が難しいです。

例えば、商品の売上を再生過程で考えようとすると、マイナスの計算ができないので支出を考えることができず適用できません。
このように、通常の再生過程はモデルがシンプルであるがゆえに、複雑なものを考えようとすると限界出てきてしまうのです。
再生報酬過程とは?
そこで登場するのが再生報酬過程です。
ここまでの内容をまとめると、再生過程の弱点を補うためには
自然数以外の色んな値を取れれば良い
ということになりますよね。

負の数も取れるようになれば、負の数を足す=引き算が実行できます!
この考えを取り入れたのが再生報酬過程です。
言葉だけで説明してもわかりにくいので具体例を通して考えましょう。
条件・設定
先ほどとは少し設定を変えて、電車の到着数ではなく到着した客が買った切符の売り上げを数えることにします。

多くの客は切符を購入していきますが、中には切符の払い戻しを求める客もいるので、その場合は売上が下がることになります。
ちなみに、このときの到着間隔 $\{X_n\}$ は乗客同士の到着間隔になります。
報酬・コスト $\{R_n\}$
通常、到着番号と切符購入・払い戻しの選択の間には依存関係がないので、1人の客からもらえる金額(報酬)は独立同分布です。
$i$ 番目に到着する客は払い戻しを求める可能性が高い、といったことは考えにくいですよね。

払い戻しが起きると鉄道会社がお金を払うことになるので、この場合は報酬ではなくコストという言葉が使われることが多いです。
そのため、$n$ 番目の客による報酬・コストを $R_n$ とすると、
$\{R_n\}_{n \in \mathbb{N}}$ は独立同分布
です。
$R_n$ は例えば次の式のように定義されます。
\begin{eqnarray} R_i = \left\{ \begin{array}{l} 500 \cdots \mbox{確率} \frac{9}{10}\\ -250 \cdots \mbox{確率} \frac{1}{10} \end{array} \right. \end{eqnarray}

たいていの客(90%)は切符を買うので500円の収入だけど、一部(10%)払い戻しのためにやってくる人がいると250円の支出になる、といった感じです。
また、到着間隔 $\{X_n\}$ と報酬 $\{R_n\}$ は独立です。
前の客が到着してから次の客が到着するまでの時間と、到着した客が払う金額(払い戻す金額)には何の関係もありませんよね。
再生報酬過程 $C(t)$
報酬・コストを表す $\{R_n\}$ を使うと、時刻 $t$ までの総売上 $C(t)$ は
$$C(t) = \displaystyle \sum_{i=1}^{M(t)} R_i$$
と表されます。
$M(t)$ まで足し合わせているのは、時刻 $t$ までの到着数が $M(t)$ だからですね。

この $C(t)$ を再生報酬過程といいます。
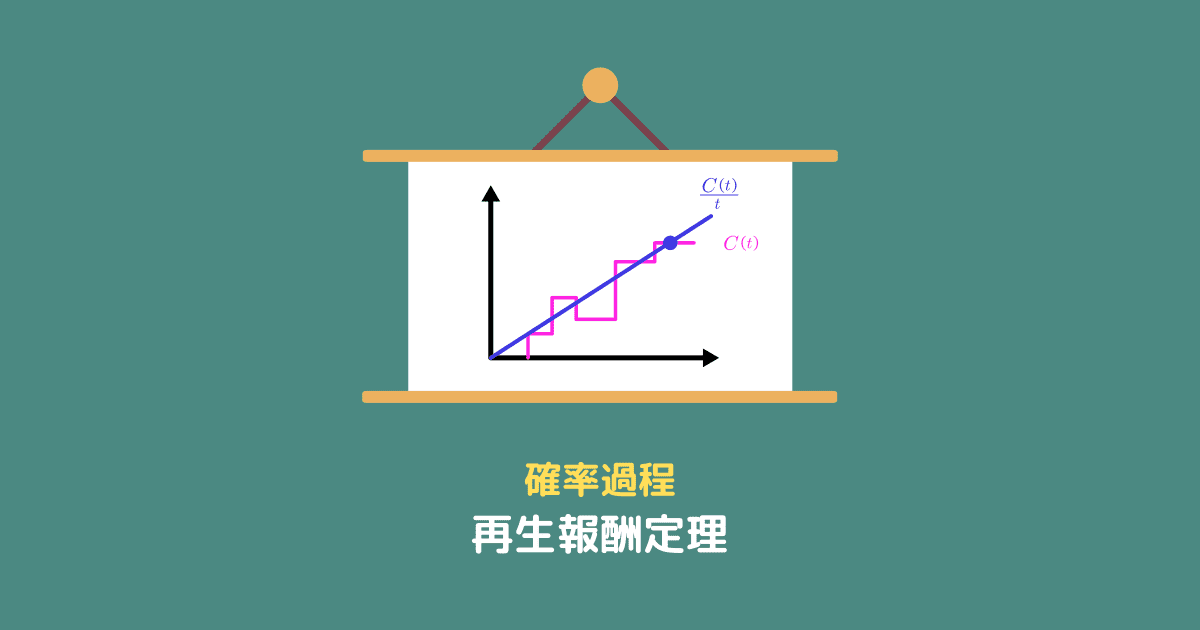
再生報酬関数 $c(t)$
再生報酬過程の期待値
$$c(t) = \mathbb{E} [C(t)]$$
を、再生報酬関数といいます。
再生報酬関数は、
時刻 $t$ までにいくら稼ぐことが期待できるか
を表しています。

再生報酬過程・再生報酬関数と再生過程・再生関数の関係はよく似ていますね。
再生報酬過程-まとめの図
今回は、再生過程を拡張した再生報酬過程をご紹介しました。
今回の内容をまとめると次の図のようになります。

再生過程との違いは、増え幅が1かそうでないかだけです!
そのため、再生報酬過程で報酬が常に1、つまり
$$\forall n \in \mathbb{N}, \quad R_n = 1$$
とした特別な場合が再生過程となります。
コメント